Thermodynamics Solutions: #2

2.* (1997 F 11) Adenine triphosphate (ATP) is the principal immediate donor of free energy in biological reactions. In a cell, ATP is being formed and consumed all the time; the typical delay between formation and consumption is approximately one minute. The turnover rate of ATP is remarkably high. A resting human consumes about 40kg of ATP in 24 hours, which is an appreciable fraction of the total body weight! A large amount of free energy is liberated when ATP is hydrolyzed to adenine diphosphate (ADP) and orthophosphate (Pi).

ATP + H2O ---> ADP + H+ +Pi   DG0 = -16.8 kcal/mol

To understand the role of ATP in free energy coupling, consider the reaction

X ---> Y    DG0 = +7 kcal/mol

A. Calculate the equilibrium constant K = [Y]/[X] for this reaction. Use R = 2cal/Kmol.

[Y]/[X] = e(-7000/(2*298)) = 7.93 x 10-6

The extremely small value of this equilibrium constant tells us that at equilibrium, there is very little Y and a lot of X. Therefore X is the more stable form.

B. Thus X cannot be spontaneously converted to Y when the molar ration of [Y] to [X] is equal to or greater than K. But X can be converted to Y when the [Y]/[X] ration is coupled to the hydrolysis to ATP. The new overall reaction is

X + ATP + H2O --> Y + ADP + H+ +Pi   DG = -9.8 kcal/mol

Where the value of DG0 for this reaction is the sum of the DG0 values for the two separate reactions. Under the conditions of a coupled reaction K’ = ([Y]/[X])([ADP][Pi][H+]/[ATP]). Find the value of K’.

Room temperature is 298K; body temperature is 310K. Either temperature was appropriate to be used in the subsequent calculations.

Room temp: K’ = e-(-9800/(2*298)) = 1.38x 107 = K’

Body Temp: K’ = e-(-9800/(2*310)) = 7.32 x 106 = K’

C. The ATP-generating system of cells maintains the [ATP]/([ADP][Pi]H+] ratio at a high level, typically on the order of 500. Use this information to calculate [Y]/[X] for the coupled reaction.

K’ = ([Y]/[X])([ADP][Pi][H+]/[ADP]) --->

[Y]/[X] = K’*[ATP]/([ADP][Pi][H+]) = 500K’

= 6.9 x 109 @ room temp

= 3.66 x 109 @ body temp

D. By comparing your results for parts A and C, determine by how much the hydrolysis of an ATP molecule changes the equilibrium ratio of [Y]/[X] when it is a coupled reaction compared to an uncoupled reaction.

At room temp: 6.9 x 109/7.93 x 10-6.

At body temp: 3.66 x 109/7.93 x 10-6.

The ratio increases by a lot!!

E. Here is a system analogous to metabolic thermodynamics. Suppose compound A is broken down into E by the following three-step reaction sequence:
 

DG0 (kcal/mol)

A + B --->> C

-3

C ---> D

-55

D ---> B + E

-32

What is the standard free energy change for the reaction A ---> E?

DG0 = -3 - 55 - 32 = -90 kcal/mol

F. Coupled to the second step is the reaction F -> G for which DG0 = +60 kcal/mol. Explain how it is possible that a reaction with DG0 of 60 kcal/mol can be made to go by one of only —55 kcal/mol.

Equimolar quantities of C, D, F, and G are not necessarily involved in the reaction.

G. Assuming equimolar concentrations of F and G, what must be the relative concentration of C and D for perfect free energy coupling between C ---> D and F ---> G reactions, that is, so that the overall DG0 value is zero?

There were three responses that received full credit for this part.

  • It is DG, not DG0, that changes with the relative concentrations of species in solution. Thus the DG0 value of zero for this sequence could not be achieved by manipulating relative concentrations.

  • If you assumed that you were meant to manipulate relative concentrations so that the DG value (not the DG0 value) for this sequence was zero, and you interpreted "relative concentration of C and D" to mean [C]/[D] instead of [C ---> D]/[F ---> G], then your calculations should look like the following.

  • If you interpreted the question as "Assuming 1:1 stoichiometry of F and G and 1:1 stoichiometry of C and D, what must be the stoichiometric ratio of [C]/[F] (or equivalently, [D]/[F], [D]/[G], [C]/[G]) for the coupled reaction if the overall DG0 value is zero?", then your calculations should look like this:

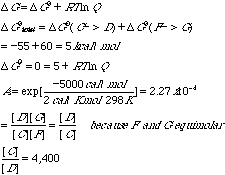
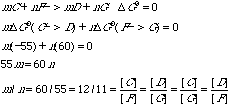
H. Demonstrate rigorously that the total free energy change in one turn of the cycle is independent of the concentrations of B, C, and D.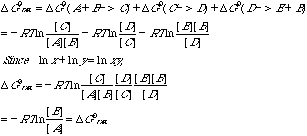