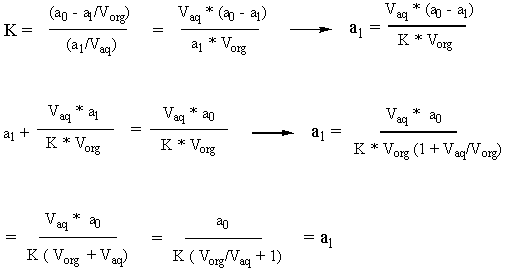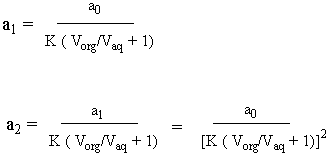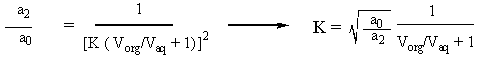Separation Technologies Solutions: #3

3.* (1996 2 8)
Note: the same problem worded slightly differently also appeared on the 2nd exam of 1993. It’s a popular problem . . .

What is the value of the minimum partition coefficient K, defined as K = [A]_org/[A]_aq that would permit removal of 99% of a solute A from 50.0 mL of water with two 20.0 mL extractions with toluene?

Note the separation "reaction" A_(aq)<------>A_(org) governed by the equilibrium constant . The partition coefficient: K = [A]_org/[A]_aq. Here toluene (methylbenzene) is the organic solvent.

Let
a₀=moles of A initially in aqueous phase
a₁=moles of A in aqueous phase after 1 extraction.
Then a₀-a₁ = moles of A in the organic phase after 1 extraction.

Let
v_aq=volume of aqueous phase
v_org=volume of organic phase for 1 extraction.

We start from the definitions of K and molarity (moles/volume). Our goal is to solve for a₂/a₀ so that we can set it equal to 0.01, meaning that 99% of a₀ is gone. But before we can get a₂ in terms of a₀, we have to get a₁ in terms of a₀. Happily, we discover that a₀ is related to a₁ by a simple factor.

This tells us that the number of moles in the in the aqueous phase after an abstraction is proportional to the number of moles in the aqueous phase before that abstraction by the proportionality constant shown above. So if we do two abstractions, the following ensues:

Therefore:

Since we want 99% of the material abstracted, we know that a₂/a₀ = 0.01. Additionally, we are given numbers for V_org and V_aq in the statement of the problem. So all we have to do is plug in the numbers and solve for K, which turns out to be 22.5.