From the questionnaires I've had requests for
indexed lists of concepts so that people can better individualize their
study patterns to target concepts that are most personally troublesome
to them. Each concept below is linked to its explication later
in this file. There are also headings to guide students who want to just
print out the whole thing. Please give me your reactions to this new
format by clicking here!!
Thermodynamics should, as Professor Zare noted, really be called "thermostatics." Thermodynamics is not about things moving and changing but instead about how stable they are in one state versus another, while kinetics is about how quickly or slowly species react. It is dangerously easy to confuse thermodynamic quantities like free energy with kinetic ones like activation energy. Probably for this reason, thermodynamics and kinetics are often taught separately.
I personally think it might make more sense to treat them
together. This way, the differences can be pointed out right from the
start, and hopefully, some of the confusion can be avoided in the first
place.
Thermodynamically favorable but kinetically unfavorable
See how much simpler it looks? What this tells you is that the products are at a lower free energy, or more stable, than the reactants. Because of this, the reactants "want" to be converted into the products. For example, graphite and diamond are both forms of carbon, but graphite has a lower free energy. Therefore, diamond wants to convert into graphite. Another example is that your skin wants to dissolve in the soap when it is washed. In this case, the products of the dissolution reaction (namely, your skin dissolved in the soap) are more stable than the reactants (your undissolved skin and the soap separately).
The above examples were chosen to specifically because even though the reaction should go (the products really are more stable than the reactants, and nature always tries to get things as stable as they can be), it doesn’t seem to. Your hands are safe when you wash them as is the diamond on your finger. Even though the reaction is thermodynamically favorable, it is slow. It’s just plain too difficult to get the diamond to break all of its bonds and re-form them in the different, more stable graphite configuration. To answer the question of why this is so we must go back to the first reaction diagram featuring the hump between reactants and products. That hump is a measure of how difficult it is to get the reaction to go in any reasonable amount of time. For diamond, the hump for the conversion into graphite is high. Even though the reaction should go thermodynamically, it does not because it is kinetically unfavorable.
Transition State
Why is the hump so high? It’s because the transition
state, or activated complex, that is at the top of the hump is so unstable
(high energy). In the case of the diamond --> graphite reaction, getting to the
transition state probably involves, among other things, breaking all the
carbon-carbon bonds in diamond. Breaking bonds always requires the
input of energy, and there are a lot of carbon-carbon bonds in
diamond. Hence the height of the hump for the diamond --> graphite
conversion.
This is the difference between thermodynamics and
kinetics. Thermodynamics can tell you only that a reaction should go
because the products are more stable (have a lower free energy) than the
reactants. Another way of saying this is that the reaction has a negative
free energy change: DG is negative and therefor the reaction is spontaneous. Yet another
way of saying this is to say that the reaction has a large equilibrium
constant, signifying that if nature could ever attain equilibrium, there
would be many more products present than there are reactants. Notice that
the DG = -RTlnK
equation says all this at once. Kinetics, on the other hand, can tell you
how fast the reaction will go but doesn't tell you anything
about the final state of things once it gets there. Consider the following
reaction sequence:
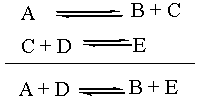
The Equilibrium Constant K
The equilibrium constant, capital K, is a thermodynamic
quantity. As such, it depends only on the overall reaction. What
the individual reaction steps that changed A and D into B and E were
doesn't matter in the slightest. Which combination is more stable: A +
D or B + E? Well, that's the one that should thermodynamically
predominate at equilibrium. Notice that the reaction intermediate C
doesn't even enter into the equation for K. For the purposes of
thermodynamic analysis, the individual steps above the overall reaction
might as well not even be there.
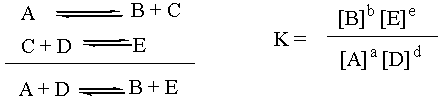
K Depends on Stoichiometry
One side note about K is that it depends on how the overall
reaction equation is written. If the stoichiometric coefficients were
multiplied by two, then the value of K for the original overall reaction
would have to be squared in order to be appropriate for the new overall
reaction. Thus, in order to determine K for a given reaction, you must be
aware of exactly which stoichiometric coefficients you are using. If a
chemist experimentally finds K for the synthesis of water from
H2 and O2 and gives her number to a colleague, and
the colleague mistakenly thinks that the reaction was written
H2 + ½O2 --> H2O instead of
2H2 + O2 --> 2H2O, then when the
colleague goes to reproduce the experiment, she will get the wrong
number. Assuming the experiment is reproducable in the first place, the
number that the colleague gets will be the square root of the number that
the original chemist got.
Solids and Liquids, Endothermic and Exothermic, Le Chatelier
A second side note about K is that pure solids and pure liquids don't get included in it. Their concentrations are so big that we can just take them as being constant throughout the reaction. Thirdly, people often analyze perturbations to equilibrium in terms of Le Chatelier's principle, which says that a system will shift to counter any change you try to make. For example, if a reaction is exothermic, that means that it gives off heat. If you raise the temperature, you are effectively adding a product to the reaction, which will cause it to shift back to the reactant side. Be careful about this though because temperature can change equilibrium constants. The change is slight, but it’s definitely there.
Kinetics and Equilibrium
Kinetics, on the other hand, does not depend in the
slightest on what the situation looks like at equilibrium. The rate of the
reaction has no dependence on the overall reaction equation but instead
depends on the reaction mechanism, the elementary steps. (This was
the part of the reaction sequence that we ignored for thermodynamics.) The
molecules on the left of each elementary step must collide in order to
react so that the products on the right are formed. Notice that in the
first step of the reaction sequence above, the reactant A doesn't have
to collide with anything. Instead, it simply breaks apart, producing B +
C. This is what is called a "unimolecular," "first order" elementary step
because only one atom is involved. In the second step of the reaction
sequence, C and D do have to collide in order to produce E. This is what
is called a "bimolecular" step because two atoms have to come together for
the reaction to occur.
Collisions
The rate of an elementary step depends on the concentration of species available to react. For example, in the second step, if there are many molecules of C and D around, then the likelihood of a molecule of C colliding with a molecule of D with sufficient energy and the right orientation to make the elementary step go is high. Therefore, the rate of the elementary step is proportional to the concentrations of the reactant molecules. Here are expressions for the rates of the two elementary steps for the reaction sequence above:
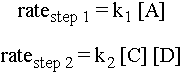
Notice that if for instance one of the elementary steps were to involve two molecules of C colliding, then the rate of that step would be proportional to [C]2.
Elementary steps of higher molecularity (termolecular and on up) are very rare because in any real scenario, it is unlikely that three molecules would hit each other in exactly the right way and with exactly enough energy for the step to happen.
The Arrhenius Equation
The rate constant k is a quantity that students love to confuse with the equilibrium constant K. Don’t do this!! K tells you the ratio of products to reactants at equilibrium while k tells you the rate of an elementary step in the reaction mechanism! Although it is most usual to find little k experimentally, it can also be found from the Arrhenius equation,
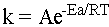
The Arrhenius equation does not tell you the rate of the reaction; it tells you the rate constant for an elementary step of the reaction. The variable Ea is the activation energy for the step, or the height of the hump on the reaction diagram at the beginning of the section. The constant R is our old friend the gas constant, and T is the temperature at which the elementary step is performed. The large sensitivity of k to T is the reason that it is extremely difficult experimentally to find rate constants. Most elementary steps either give off or take up heat, and the resulting temperature change changes the rate of the elementary step itself. Thus, the practical utility of the Arrhenius equation is limited.
The constant A is the "Arrhenius factor." It takes into account the fact that molecules not only must collide, they must collide with the right orientation. When you take Chem 33, you will learn that for some reactions classified as "SN2" the collision must involve one molecule putting electron density into an antibonding orbital on another molecule. This is a very precise place to have to put electron density! Therefore, only a small fraction of collisions result in reaction. The Arrhenius factor is also called an "entropic factor" to stress that it accounts for how random collisions can be if they are to result in a reaction.
Finding Rate Laws and k From Empirical Data
From experimental data, it is often possible to find the rate law for a reaction. For example, given the following numerical data, you can deduce that the overall reaction is first order in A, first order in B, second order in C, and that the rate constant is 6 x 102 M-3s-1. This is because the rate of reaction doubles when you double the concentration of either A or B (leaving all other initial concentrations constant) and quadruples when you double C (leaving all other initial concentrations constant). Once you know the exponents, you can plug in to the equation to obtain k. Keep in mind that this procedure finds the initial rate of the reaction. Often, as the reaction progresses, the rate changes.
|
Experiment |
[A] |
[B] |
[C] |
rate |
|
1 |
0.1 |
0.1 |
0.1 |
6 x 10-2 |
|
2 |
0.1 |
0.1 |
0.2 |
2.4 x 10-1 |
|
3 |
0.1 |
0.2 |
0.1 |
1.2 x 10-1 |
|
4 |
0.2 |
0.1 |
0.1 |
1.2 x 10-1 |
Rate = 6.0 x 102 [A][B][C] 2
Bottlenecks
We've discussed the rate of individual elementary steps of a reaction, but how do we find the rate of an overall reaction? One way to do this is to realize that the rate of the reaction will be determined by the rate of its slowest step. If there is a long line at the ATM but no line at the coke machine next to it, then the rate of your getting a coke is pretty much the same as the rate of your getting money out of the ATM. Consider again what is fast becoming our favorite reaction sequence:
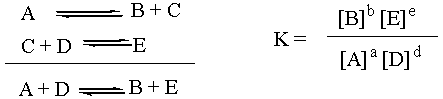
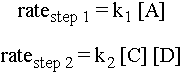
If the first elementary step is standing in line at the ATM and the second step is getting a coke, and if it takes a long time to get money but relatively little time to get a coke, then we can write that the rate of the entire reaction (here modeled by the coke-obtaining process) is equal to the rate of the first elementary step:
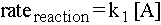
Note that there is no way we could have predicted which step would be the slowest. The bottleneck step must be determined experimentally. If there were a long line at the coke machine but no line at the ATM, then the rate of the overall reaction would be the rate of the second elementary step:
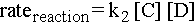
The Steady State Approximation
However, it is considered bad form to write the rate of an overall reaction in terms of a reaction intermediate. Reaction intermediates are constantly being created and being consumed, so [C] varies greatly from time to time during the reaction. We can get around this by using what is called the "steady state approximation" to solve for [C] in terms of the concentrations of the other reactants.
In order to understand the steady-state approximation, we have to realize that thus far we have only considered the rate of an elementary step going forward. Each elementary step has a corresponding back reaction that also has an associated rate. The real situation can be represented as follows:
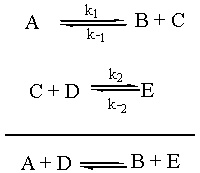
We are going to assume that the rate of change of the concentration of the intermediate C, d[C]/dt, is approximately zero. (This is why it is called the "steady state approximation.") Now, d[C]/dt is equal to the rate of formation of C, k1[A] + k-2[E], minus the rate of destruction of C, k-1[B][C] + k2[C][D]. So the math for this scenario is as follows:
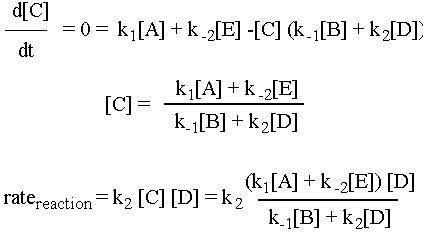
Pretty complicated rate expression, eh?! Depending on what tricks you use (the steady state approximation is just one of them) you can get some very crazy expressions. See for example Professor Zare’s lecture example of H2(g) + Br2(g) à 2HBr(g). If you understood the preceding example, you already understand all of the important ideas behind Michaelis-Menton kinetics. Michaelis-Menton does the same steady-state approximation math for a biological enzyme-substrate system.
Michaelis-Menton
Enzymes are special proteins that catalyze biological reactions. Many enzymes break down food molecules into material from which your body can get energy. The enzyme (called E) has a little niche into which the substrate food molecule (called S) fits just perfectly. When it gets into the enzyme’s protective cleft, it is broken down into the usable-for-energy product (called P). We can represent the system as follows:

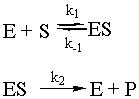
To solve this system, use the fact that the second step is the slow step to invoke the steady-state approximation. You will also use the all-important fact that [E] = [Eo] – [ES], where Eo is the initial amount of enzyme. Note that there is no k-2 for this reaction: the enzyme will not catalyze the conversion of the product back to the substrate. Given all of these constraints, the math looks like what follows. To make sure that you understand it, try to reproduce the answer from the given reaction sequence and the constraints detailed in this paragraph.
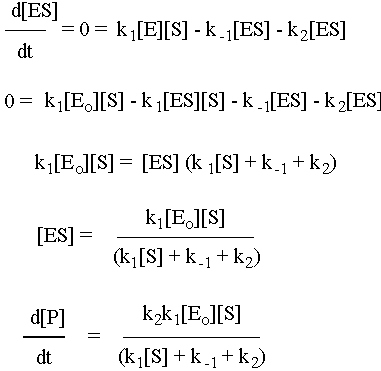
Michaelis-Menton Limiting Cases
If [S] is really big (i.e. [S] >> k-1 + k2), then d[P]/dt = k2 [Eo], which is effectively a zero-order reaction because k2 and [Eo] are both constant. So, as in the kinetics problem set, if you know the rate constant for the second elementary step (k2) and you’re also given the rate of the zero-order product formation reaction (d[P]/dt), then you can solve for [Eo], which is the enzyme (on the problem set that was LADH).
Integrated Rate Laws
The last topic to consider before we leave kinetics and go back for a last look at thermo is integrated rate laws. Given the elementary steps, it is possible to integrate the corresponding rate law, using calculus to solve for the concentration of some reaction species as a function of time. Test yourself heavily on both first order and second order rate law integration. From the equation for the elementary step, you should be able to figure out the concentration of the species as a function of time. Remember, this is just math. The chemical parts are only the first line and the last line of each derivation. Here are the answers you should be able to derive:
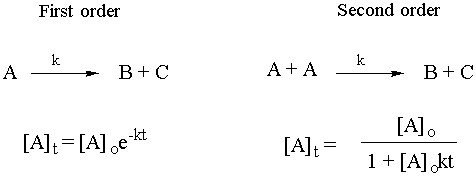
Actively test yourself on this!! You may be able to follow all the math, but could you reproduce it? It’s also important to have a feel for what is happening chemically for first order and second order reactions.
Common examples of first order reactions are radioactive decay
processes. As must be the case for first order reactions, the rate of
decay depends on the amount of radioactive stuff that's around at any
one time. This results in an exponential decrease in the decay rate with
time. When less stuff is around, it does not decay anywhere nearly as
fast.
When chemists talk about radioactive decay, they typically like to talk
about half-lives. The half life of a substance is how long it takes for
half of whatever's there to decay. At time t1/2,
[A]t1/2= (1/2) [A] o. Therefore, if you bring the
[A]o over to the left side of the first order equation, the left side
becomes simply ½. Thus you have ½ = e-kt. Take the
natural log of both sides and solve for t1/2to obtain
t1/2= .7/k.
Summary of the differences between K and k:
|
K |
Little k |
|
Thermodynamic, not kinetic |
Kinetic, not thermodynamic |
|
K doesn't really have units, though we often treat it as if it does. |
Rate constant changes with T and with catalyst. A catalyst would change the activation energy for the rate-determining step. |
|
K is independent of the reaction mechanism. It is written from the products and reactants in the final, overall reaction equation. |
You can't know the rate law until you know the reaction mechanism and have identified the slowest step (the bottleneck). Only reactants appear in the rate law. |
|
Don't include solids or pure liquids in K because their essentially-constant concentrations are already absorbed into the equilibrium constant. |
Intermediates are of fleeting existence, so it doesn’t make sense to leave their concentrations in the final rate law. Use the steady-state approximation. |
|
The value of K depends on the stoichiometric coefficients of the equation to which it is referenced. |
|
|
Equilibrium may take a long time to be achieved! |
|
|
Le Chatelier: for exothermic reactions, heat is a product; for endothermic reactions, heat is a reactant. |
|
Free Energies and Electrochemistry
Now back to thermo to wrap up this integrated discussion of thermodynamics and kinetics. The last thing to talk about with respect to thermodynamics is free energies and electrochemistry. It is usually not a temptation to mix these topics up in kinetics, which is why they are tacked on the end in this section.
There are three main kinds of free energy:
- U = q – wPV – welec = heat in minus work out (or equivalently, heat in plus work in). Note that wPV is pressure volume work and welec is electrical work.
- H = U + PV = enthalpy. Note that if a reaction has a negative enthalpy
change, it is exothermic and if it has a positive enthalpy change it
is endothermic. Note also that breaking bonds is always endothermic
(positive DH)
and forming them is always exothermic (negative DH). In common terms, it
always takes energy to break bonds and it always releases energy to
form them.
- G = H-TS. If you take the delta of both sides and do the math for this
situation you come out with DG = welec, or electrical
work. Note that q = TDS and we are assuming volume is constant, so that DV = 0. The math is shown
below:
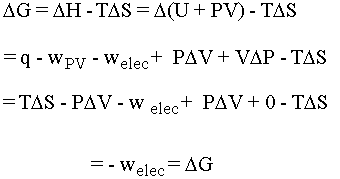
Notice that the heat flow TDS and the pressure-volume work terms cancel so that at constant temperature and pressure we are left simply with electrical work. For us, this means work that a chemical system can do by causing electrons to flow. The oxidation states of the chemicals in the system change as the electrons flow between them (more on this when we do redox). If we put the chemical that wants to give up electrons into one beaker and the chemical that wants to take electrons into another beaker we can force the electrons to flow along the wire connecting them (and light up a lightbulb or something along the way . . .). This is the principle behind an electrochemical cell. Be cognizant of the following equations and what they are telling you:
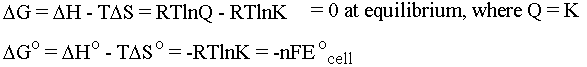
The cell potential E0cell is measured in
Volts. Note that DGo is defined to be the amount of electrical work
you can get out of the system when you start with every
concentration being 1M. (Note also that this is one of those cases
where we can't treat K as though it had units, because you can't
take the log of anything that has units.) E0cell
is "reduction potential," which is a measure of how much a species
wants to be reduced at STP. If a chemical really wants to be reduced
(gain electrons) then it's a good oxidizer (loser of
electrons). Also in these equations, n is the number of moles of
electrons that is flowing, F is the Faraday constant in coulombs per
mole, and E0cell has units of Joules/Coulomb,
which makes it work out so that DG has units of Joules/mole, as it
should. Since negative DG signals a spontaneous reaction, it follows that positive
E0cell signals a spontaneous reaction
too. E0cell = E0oxidized
substance - E0reduced substance for a total
reaction, but it is important to realize that if you're not doing a
total reaction but instead using the E0's to calculate the
E0cell for a new half-cell, you have to go
through DG. Professor Zare gave a handout on the mathematical reason why
this is so; it boils down to the fact that DG is what is called a "state function" and
E0 is not. Like DG, positive E0cell is a thermodynamic
quantity.