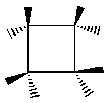
Group TheoryNote: there is another very different and very good introduction to group theory here. Check it out! Symmetry operations are acts of rotating or reflecting a molecule or figure. Symmetry elements are the symmetry operations that can be done on a molecule to leave it indistinguishable from the way it was when you started. If we say that a molecule has symmetry C4 about a given axis, we mean that 4 equal rotations (of 90 degrees each) about that axis will get us back to where we started, and that each of the four rotations will leave the molecule in a position identical to its starting position. Cyclobutane has a C4 axis coming out of the page. If Java is enabled on your browser, you can rotate the figure below by clicking and dragging with your mouse. Notice also the reflection plane (reflection planes are denoted with the Greek letter s, or sigma) that starts out in the plane of the molecule. Move the figure around see if you can make the atoms line up so that the reflection plane is perpendicular to the page.
Note that in these interactive figures, the bonds are not shown. Only the atoms are there. I have colored carbon red and hydrogen blue for your viewing pleasure. You should learn to recognize the different ways that chemists represent three-dimensional structures on two-dimensional paper. Here is a drawing of cyclobutane as a chemist might sketch it. Notice that the bold lines indicate bonds that come out of the page and the dashed lined indicate bonds that go into the page. This shows that the four carbon atoms approximately define a plane; the hydrogens are on either side of the plane. Even though carbons are singly-bonded to each other, there is not free rotation about this carbon-carbon bond because there isn't room for the hydrogens to squeeze past each other though the ring.
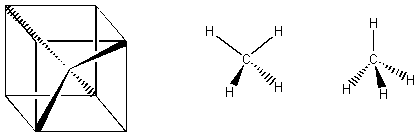
 If a molecule has symmetry C3 about some axis, we mean that three equal rotations (of 120 degrees each) about that axis will do the same thing. Methane, a tetrahedral molecule, is shown below. Can you find its C3 axes? Use your mouse to turn the molecule so that one of the blue hydrogens is pointing toward you. Now do you see the C3 axis? Methane also has 6 reflection planes. Each reflection plane is defined by the central carbon and two of the hydrogens.
Here are some alternate representations of methane. The first shows explicitly that the four lobes of the tetrahedron point toward the corners of a cube. The other two use the conventions that bold means out of the page and dashed means into the page. The drawing to the far right has one of the C3 axes of methane in the plane of the page.
 All symmetry operations are some combination of rotations and reflections. However, sometimes we do what is called an "improper rotation" in which we rotate the molecule and then reflect it through a plane perpendicular to the axis of the rotation. So, for example, an S4 is just like a C4 except that after rotating the molecule 90 degrees about some axis, we reflect it through a plane perpendicular to that axis. The methane molecule above has an S4. The Official Chem 32 Theme Molecule, allene, also has an S4. Allene is pictured below. Notice that if you were to replace just one of the hydrogens with a heteroatom such as chlorine, the S4 symmetry is destroyed.
One of the reasons allene is so popular in this class is that it is not only interesting from a group theoretical perspective, but also from a bonding perspective. The central carbon is sp hybridized. Its two unhybridized p orbitals are required by quantum mechanical laws to be perpendicular to the sp hybrid orbitals and to each other. The consequence is that the sp hybrid orbitals on the central carbon form sigma bonds with the two outer carbons, one pi bond is formed in the plane of the page, and the other pi bond is perpendicular to the plane of the page. Below is a projection down the carbon-carbon-carbon bonds of allene and a picture of the p orbitals that are involved in its bonding scheme. Notice that you can only see the tops of the p orbitals on the left; they are coming out of the page. This type of system, in which two adjacent pi bonds are formed from perpendicular sets of orbitals, is called a cumulated system and is somewhat unstable (although allenes are found in nature). Later we will contrast such systems with their more stable, conjugated counterparts.
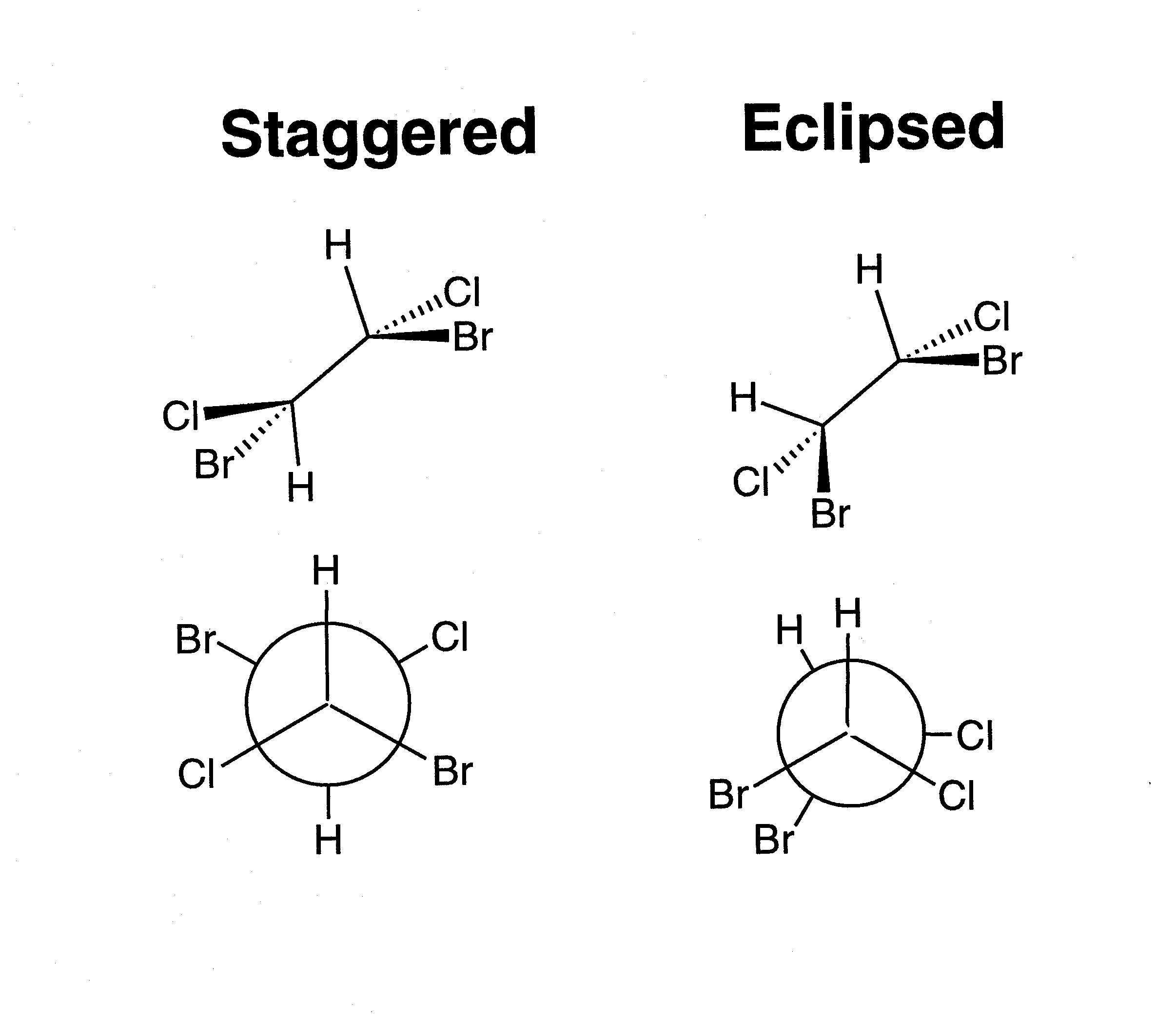
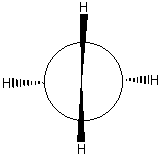 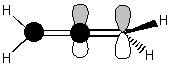 Chemists often talk about "inverting" a molecule (or orbital) or of its having even or odd "inversion symmetry." A molecule that is even to inversion has the property that if you take every point in the molecule, pass it through the molecule's center, and bring it out the same distance on the other side, the molecule will be unchanged. An orbital that is odd to inversion has the property that if you take every point of that orbital, pass it through the orbital's center, and bring it out the same distance on the other side, the sign of the orbital's wavefunction will be inverted (i.e. its shading will be flipped). "Inverting" a molecule is the same as doing an S2 improper rotation. Notice that a simple reflection is also the same as doing an S1 improper rotation. These two facts become especially useful when we talk about chirality. Chiral molecules are defined as molecules that have no improper rotation axes. So if a molecule has reflection or inversion symmetry in any of its conformations, then you immediately can tell that the molecule is not chiral. All of the moveable molecules featured above do have reflection or inversion symmetry, so none of them are chiral. You may have heard of chiral molecules before and been told that a chiral molecule is a molecule having a carbon with four different substituents (such a carbon is often called a "chiral center"). This is usually a good rule of thumb, good enough for most non-chem 32 students anyway!! However, now that you know the group theoretical definition of chirality, you know that there is more to it than that. For example, look at the molecule of 1,2-dibromo 1,2-dichloroethane below. Each of the carbon atoms has four different substituents. However, since the carbon-carbon bond is a single bond, there is free rotation about that bond. You could line up the atoms to show a mirror plane or an inversion center as in the pictures below. If a molecule has reflection or inversion symmetry in any of its conformations, it is achiral. When we look down the carbon-carbon bond as in the bottom figures (these are called "Newman projections") the inversion symmetry in the "staggered conformer" and the mirror reflection plane in the "eclipsed conformer" are especially evident.
 And while we're dispelling introductory chemistry myths, what about the substituted allene molecule below? This is a molecule that most certainly does not possess a carbon with four different substituents--each carbon has a double bond!! However, it does not possess reflection symmetry, inversion symmetry, or any other higher-order improper rotation axes either. This is a chiral molecule without a chiral center.
(It is worth noting on the side that just because you don't see any reflection planes or inversion centers, you cannot immediately say a molecule is chiral. There might be a higher-order improper rotation axis that renders the molecule achiral. This is extremely rare.)
Why all this fuss about whether a molecule is "chiral" or not? Chiral
molecules have the property that they are "handed." Just as you only
shake hands right-hand to left-hand, chiral molecules in your body can only "shake
hands" (i.e. interact) with certain other chiral molecules. This has
far-reaching biological implications that we will explore. Your
enzymes, for example, are chiral proteins that are evolutionarily primed to
recognize very specific molecules in very specific chiral configurations.
We will talk about this extensively later; the point of this section is
simply to make sure that you will be able to recognize chiral molecules
when they come up.
Also, chiral molecules have the physically interesting property that they
rotate plane polarized light. In fact, this is how they were first identified. Louis Pasteur, a French chemist, was puzzled by the fact that crystals that formed on some wine bottles rotated plane polarized light in opposite directions. By coincidence, the crystals themselves were handed too, and Pasteur was able physically to separate the ones that rotated light clockwise from the ones that rotated it counterclockwise. Jean Baptiste Biot, the deal of French optical rotation studies, was skeptical and made Pasteur do it in front of him before he believed the result. It was a great moment in the history of chemistry.
We can symmetrically classify a molecule or orbital in terms of its
point group. Molecules in the same point group have the same
symmetry elements. Professor Zare has provided a decision tree that you
can use to decide what point group to put a molecule into. Another option is to internalize the following classification scheme.
There are four sets of point groups. The first is for
molecules with low symmetry: C1 (only E), Cs (only E and sigma), and Ci
(only E and I). The second is for molecules with high symmetry: Td,
(tetrahedral), Oh (octahedral), and Ih (icosohedral). If a molecule
doesn't fall into the low symmetry groups or the high symmetry
groups, then it is in either one of the Cn groups or the Dn groups. The
difference is that a molecule in a Dn group has n C2 axes perpendicular
to the principle axis, where n is the order of the principle axis. The
subscripts are as follows: if there is a sigma h (perpendicular to the
principle rotation axis), add an h; if there is no sigma h but a sigma v
(containing the principle rotation axis), add a v; if there are no
reflection planes, don't add a subscript. One more rule: there is
no such thing as a Dnv point group, so if you have this, call it instead
a Dnd molecule. The official definition is that
if the v planes bisect C2 axes, then these are dihedral reflections, and
are denoted d.
The only way to really understand point groups is to get lots of practice. Look at the molecules below and think about what point group you would assign. Move them around with the mouse and look at them from different angles to make sure you don't miss any of their symmetry elements. Some of them are very difficult! When you get the hang of it, this can be fun (in a sick sort of way . . .). You may find yourself unable to stop assigning point groups; to leaves, to window panes, to Professor Collman's fishing rod pointer and Professor Zare's eyeglasses . . .
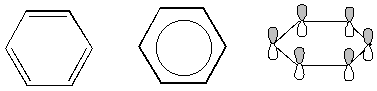
Below are some alternative representations of benzene. The last one shows the p orbitals making up benzene's conjugated system. (A conjugated system is a system in which there are alternating double and single bonds. Recall that a cumulated system, like allene, has adjacent double bonds. Conjugated systems are very stable while cumulated systems are somewhat unstable for reasons that we will study soon in the organic chemistry section.)
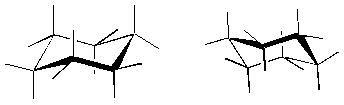
Below are some alternative representations of cyclohexane. Notice that unlike benzene, cyclohexane is not flat, but adopts a puckered shape that chemists refer to as a "chair." Below are two conformations of benzene. We will not go into how they differ and how they interconvert, but trust me, it's very cool.
Note that ethane has two conformations with appreciable symmetry: one in which the hydrogen atoms are eclipsed and another in which they are staggered. In the figure above they are staggered. Use the mouse to get the picture to look like the Newman projection for staggered ethane that we looked at earlier. The conformations differ only by rotation about the carbon-carbon bond, which happens easily at room temperature. Just for fun, try to imagine what the symmetry elements would be for both conformations.
If you can find all the symmetry elements of buckminsterfullerine (a.k.a. The Bucky Ball), then you know you understand this section!!! Buckminsterfullerene is an icosahedron.
Following is a summary of the chemical applications of group theory that
we will explore in this course. Note that these are only a few of the
possibilities; group theory can be extremely powerful when it is applied
to chemical systems. In fact, there is a whole book titled Chemical
Applications of Group Theory that you will encounter if you continue
on in physical and inorganic chemistry. As you delve deeper into science
and math, you will gain an increasingly deep appreciation for the power
and beauty of symmetry in the universe. But before I start waxing
philosophical, here's that list:
Only molecules belonging to the Cn, Cnv, and Cs point groups
are polar, which means that they have a dipole moment.
You can usually tell just by looking at a molecule whether it has a
dipole moment, but it's always nice to be able to back it up
mathematically. And sometimes it's not so obvious from inspection. For example,
tetrahedral molecules such as carbon tetrachloride (CCl4) are
non-polar despite the four very electronegative chlorines pointing
off in different directions. If you were to calculate the dipole
moment vectors, they would cancel each other out. But if you don't
want to do the calculation, it's helpful to just know from group
theory that tetrahedral molecules are non-polar and leave it at
that.
|