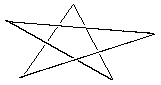
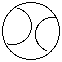Group Theory Solutions: #1

1. Identify the point group of each of the following pictures. Which are chiral? Which have dipole moments?

There is a 5-fold rotation axis perpendicular to the plane of the page. There are 5 C₂ axes perpendicular to the principal rotation axis, so this is a D group. There is a mirror plane in the plane of the page (perpendicular to the principle rotation axis), so this group is D_5h, which is not chiral or polar. Notice that using the simplified search criteria, we didn't need to list out all of the symmetry elements that the picture has in order to decide on a point group (clearly there are improper rotations, etc.).

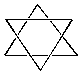
There is a 6-fold rotation axis perpendicular to the plane of the page. There are 6 C₂ axes perpendicular to the principal rotation axis, so this is a D group. There is a mirror plane in the plane of the page (perpendicular to the principle rotation axis), so this group is D_6h. Notice that unlike the picture in part a, this picture has an inversion center. An interesting trivia fact is that all the D_nh groups where n is even have an inversion center; the D_nh groups where n is odd do not. In any case, no D_nh group molecule is polar or chiral.

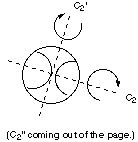
Given this baseball (and assuming it looks the same from behind), we have the following symmetry elements:

We also have mirror planes containing all three axes. Therefore the point group of this picture is D_2h, which is neither chiral or polar.

This linear picture has a C-infinity rotation axis along the axis of the pencil and no inversion center. Therefore the pencil is C-infinity-v. This is not a chiral group, but it is polar.